问题
填空题
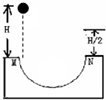
图示M、N是固定的半圆形轨道的两个端点,轨道半径为R,一个质量为m的小球从M点正上方高为H处自由落下,正好沿切线进入轨道,M、N两点等高,小球离开N点后能上升的最大高度为H/2,不计空气阻力,则小球在此过程中克服半圆轨道摩擦力做的功为______;小球到最高点后又落回半圆轨道,当它过最低点上升时,其最大高度的位置在M点的______(填“上方”、“下方”或“等高处”).
答案
对全过程运用动能定理得,mg(H-
)-Wf=0,解得Wf=H 2
.mgH 2
因为第二次通过半圆轨道克服摩擦力做功小于
.根据动能定理得,mgH 2
mg(
-h)-Wf′=0,因为Wf′<H 2
,h>0,知最大高度的位置在M点的上方.mgH 2
故答案为:
上方mgH 2
