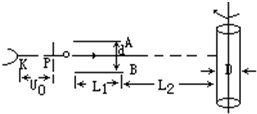
理论研究指出,简谐振动的振动位移X与时间t的关系图象(x-t)可以是一条余弦曲线,其函数表达式为:x=Acosωt,其中A是振幅,ω=2π/T.对于周期性变化的电压和电流的图象也可以是一条余弦曲线,其函数表达式类似.下图中从阴极K发射的电子经电势差U0=5000V的阳极加速后,沿平行于板面的方向从中央射入两块长L1=10cm、间距d=4cm的平行金属板A、B之间,在离金属板边缘L2=75cm处放置一个直径D=20cm、带有记录纸的圆筒.整个装置放在真空内,电子发射的初速度不计(见图).若在两金属板上交变电压以U2=1000cos2πt(V)的规律变化,并使圆筒绕中心轴按图示方向以n=2转/s匀速转动,电子质量为9.1×10-31kg,电子电量为1.6×10-19c求:
(1)电子加速后的入射速度?
(2)在纸筒上的落点对入射方向的总偏距?
(3)确定电子在记录纸上的轨迹形状并画出1s内所记录到的图形.
(1)电子在加速电场中,由动能定理得:
eU0=
m1 2 v 20

得电子加速后的入射速度 v0=
=4.2×107m/s2eU0 m
(2)加上交变电压时,A、B两板间运动时:
电子飞离金属板时的竖直偏转距离 y1=
a1 2
=t 21
•1 2
(eE2 m
)2L1 v0
电子飞离金属板时的竖直速度 vy=at1=
•eE2 m L v0
电子从飞离金属板到达圆筒时的偏距
y2=vyt2=
•eE2 m
•L v0
=L2 v0 eE2L1L2 m v 20
所以在纸筒上的落点对入射方向的总偏距为
y=y1+y2=(
+L2)L1 2
+L2=(eE2L1 m v 20
+L2)L1 2 L1U2 2dU0
代入解得,y=0.20cos2πt(cm)
(3)在记录纸上的点以振幅0.20m,周期T=
=1s而做简谐运动,因为圆筒每秒转2周,故在1 s内纸上的图形如图所示.2π ω
答:
(1)电子加速后的入射速度是4.2×107m/s.
(2)在纸筒上的落点对入射方向的总偏距是0.20cos2πt(cm)
(3)确定电子在记录纸上的轨迹形状并画出1s内所记录到的图形如图所示.
