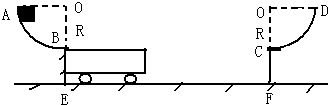
如图所示,固定在地面上的光滑轨道AB、CD,均是半径为R的
圆弧.一质量为m、上表面长也为R的小车静止在光滑水平面EF上,小车上表面与轨道AB、CD的末端B、C相切.一质量为m的物体(大小不计)从轨道AB的A点由静止下滑,由末端B滑上小车,小车在摩擦力的作用下向右运动.当小车右端与壁CF接触前的瞬间,物体m恰好滑动到小车右端相对于小车静止,同时小车与CF相碰后立即停止运动但不粘连,物体则继续滑上轨道CD.求:1 4
(1)物体滑上轨道CD前的瞬间时速率;
(2)水平面EF的长度;
(3)当物体再从轨道CD滑下并滑上小车后,如果小车与壁BE相碰后速度也立即变为零,最后物体m停在小车上的Q点,则Q点距小车右端多远?
(1)设物体从A滑至B时速率为Vo,根据机械能守恒定律有:mgR=
mvo21 2
vo=2gR
物体与小车相互作用过程中,系统动量守恒,设共同速度为V1,有:mvo=2mv1
解得物体滑上轨道CD前的瞬间时速率:v1=2gR 2
(2)设二者之间的摩擦力为f,根据动能定理有,
对物体有:-fSEF=
mv12-1 2
mvo21 2
对小车有:f(SEF-R)=
mv121 2
(或对系统根据能量守恒定律有:fR=
mvo2-1 2
2mv12)1 2
得f=
mg1 2
SEF=
R3 2
(3)设物体从CD滑下后与小车达到相对静止,共同速度为V2,相对小车滑行的距离为S1,小车停后物体做匀减速运动,相对小车滑行距离为S2,根据动量守恒和能量守恒有:
mv1=2mv2
fS1=
mv12-1 2
2mv221 2
对物体根据动能定理有:fS2=
mv221 2
解得S1=
RS2=1 4
R1 8
则Q点距小车右端距离:S=S1+S2=
R3 8
答:(1)物体滑上轨道CD前的瞬间时速率v1=
.2gR 2
(2)水平面EF的长度为
R.3 2
(3)最后物体m停在小车上的Q点,则Q点距小车右端
R.3 8
