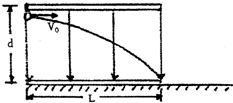
（1）带电粒子的初速度为v₀时，

     水平方向：L=v₀t₁

     竖直方向：d=

1

2

a

t

21

联立得到，d=

1

2

a(

L

v0

)2

带电粒子的初速度变为2V₀时，

    水平方向：L=2v₀t₂

    竖直方向：y=

1

2

a

t

22

联立得到，y=

1

2

a(

L

2v0

)2=

1

4

d

（2）带电粒子的初速度变为2v₀，粒子离开电场时速度的偏向角为φ．根据推论可知，粒子离开电场时速度的反向延长线交于上板的中点．则根据几何知识有

   tanφ=

d 4

L 2

=

d

2L

，又tanφ=

d

LAB

  

 解得 L_AB=2L

所以x=0.5L+L_AB=2.5L

（3）根据动能定理得，

v0入射时：qu=Ek1- 1 2 m v 20 2v0入射时：q u 4 =Ek2- 1 2 m(2v0)2

由第（1）问d=

1

2

a(

L

v0

)2，a=

qu

md

得

刚好贴着下板边缘飞出有： d= quL2 2m v 20 d

联立解得：

Ek2

Ek1

=

d2+4L2

4d2+L2

答：

（1）带电粒子的初速度变为2V₀，离开电场时，沿场强方向的侧向位移y为

1

4

d．

（2）带电粒子的初速度变为2V₀，粒子离开电场后继续运动，当它的竖直位移仍为d时，它的水平位移x为2.5L．

（3）如果带电粒子的初速度变为2V₀，粒子离开电场时动能与带电粒子以初速度V₀射入匀强电场后离开电场时动能之比

Ek2

Ek1

=

d2+4L2

4d2+L2

．