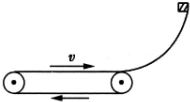
如图所示,一水平方向的传送带以恒定速度v=2m/s沿顺时针方向匀速转动,传送带右端固定着一光滑的四分之一圆弧轨道,并与弧下端相切.一质量m=1kg的物体自圆弧轨道的最高点由静止滑下,圆弧轨道的半径尺R=0.45m,物体与传送带之间的动摩擦因数μ=0.2,不计物体滑过曲面与传送带交接处时的能量损失,传送带足够长,取g=10m/s2.
(1)求物体从第一次滑上传送带到离开传送带所经历的时间;
(2)求物体从第一次滑上传送带到离开传送带的过程中,传送带对物体做的功及由于摩擦产生的热量;
(3)求物体从第二次滑上传送带到离开传送带的过程中,传送带对物体做的功及由于摩擦产生的热量;
(4)经过足够长的时间之后物体能否停下来?若能,请说明物体停下的位置;若不能,请简述物体的运动规律.
(1)物体沿圆弧轨道下滑的过程中机械能守恒,设物体滑到传送带右端时的速度为v1,则有:
mgR=
mv12.1 2
解得v1=3m/s.
物体在传送带上运动的加速度大小为a=
=μg=2m/s2.μmg m
物体在传送带上向左运动的时间t1=
=1.5s.v1 a
向左运动的最大距离s=
=2.25m.v12 2a
物体向右运动达到速度为v时,向右运动的距离s1=
=1m.v2 2a
所用的时间t2=
=1s,匀速运动的时间t3=v a
=0.625s.s-s1 v
所以t=t1+t2+t3=1.5+1+0.625s=3.125s.
(2)根据动能定理得,传送带对物体做的功
W=
mv2-1 2
mv12=-2.5J.1 2
物体相对传送带滑过的路程△x=
+v(t1+t2)=6.25mv2-v12 -2a
由于摩擦产生的热量Q=μmg•△x=12.5J.
(3)根据机械能守恒定律,物体第二次滑上传送带时的速度为2m/s.
物体先向左做匀减速运动,减速到速度为零,然后向右做匀加速运动,直到速度变为v=2m/s.
时间t4=2
=2s.v a
根据动能定理,由于物体从滑上传送带到离开传送带过程中物体的动能没有变化,故传送带对物体所做的功W2=0.
在这段时间内物体相对传送带滑过的路程△x2=vt4=4m
所以由于摩擦产生的热量为
Q′=μmg•△x2=0.2×1×10×4J=8J.
(4)物体不会停下来,物体在圆弧轨道和传送带上做周期性往复运动.
