问题
问答题
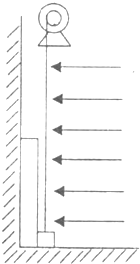
如图所示,一长绝缘木板靠在光滑竖直墙面上,质量为m.木板右下方有一质量为2m、电荷量为+q的小滑块,滑块与木板间的动摩擦因数为μ,木板与滑块处在场强大小为E=4mg/q的匀强电场中,电场方向水平向左,若电动机通过一根绝缘细绳拉动滑块,使之匀加速向上移动,当滑块与木板分离时,滑块的速度大小为v.此过程中电动机对滑块做的功为W.(重力加速度为g).
(1)求滑块向上移动的加速度大小;
(2)写出从滑块开始运动到与木板分离的过程中木板增加的机械能随时间变化的函数关系式.
答案
(1)滑块与木板间的正压力大小为
FN=qE=4mg
F=μFN
对滑块W0一2mgh-Fh=
•2mv2 1 2
v2=2ah
由以上几式解得a=(1+2μ)mgv2 W0-mv2
(2)对长木板由牛顿第二定律得
F一mg=ma′
摩擦力对木板做功为W=Fx
x=
a′t21 2
根据功能关系木板增加的机械能等于摩擦力所做的功,即△E=W
由以上各式解得△E=2(4μ一1)μmg2t2
答:(1)滑块向上移动的加速度大小为
;(1+2μ)mgv2 W0-mv2
(2)从滑块开始运动到与木板分离的过程中木板增加的机械能随时间变化的函数关系式为△E=2(4μ一1)μmg2t2.
