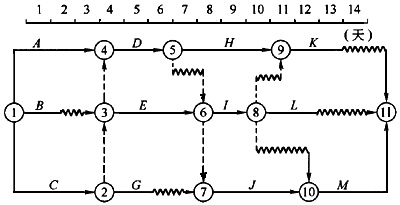
如图,传送带与地面倾角θ=37°,逆时针转动,并以v0=10m/s的速度运行着,在传送带上端A处轻轻放一质量m=0.5kg的物体,C处是物块速度等于皮带速度这一瞬间.它与传送带之间的动摩擦因数μ=0.5,AB间长度L=16m,则把物体送到B点时的速度是多少?某学生审完题后用动能定理列出下式:
limgsinθ-Lμmgcosθ=
mvB2-1 2
mvA21 2
VB=[2Lg(sinθ-μcosθ)]1/2=…
上述结果是否正确?若正确,列式证明;若错误,求出正确结果.均要有文字说明.(sin37°=0.6 cos37°=0.8)
该同学结论错误.由于初始皮带速度大于物块速度,物块相对皮带向上,故皮带对物块的摩擦力沿斜面向下,摩擦力做正功,物块动能增大.当物块速度等于皮带速度这一瞬间,物块相对皮带速度为零,瞬时摩擦力也为零,但由于物块将要继续加速,所以皮带给物块的摩擦力方向为沿斜面向上,一直到物块运动到B端.
正确解法:设物块到达C点的速度vC与皮带速度相等,AC间的距离为s1,则由动能定理得
(mgsinθ+μmgcosθ)s1=
mvC2-1 2
mvA2 ①1 2
(mgsinθ-μmgcosθ)(L-s1)=
mvB2-1 2
mvC2 ②1 2
由①式得:
s1=
=5mvC2-vA2 2g(sinθ+μcosθ)
①+②式得:
Lmgsinθ+(2s1-L)μmgcosθ=
mvB21 2
解得:vB=
=12m/s2g[(Lsinθ+2s1-L)μcosθ]
答:上述结果是错误的,把物体送到B点时的速度是12m/s.