问题
问答题
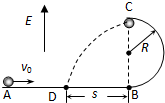
如图所示,竖直平面内有一半径为R的半圆形光滑绝缘轨道,其底端B与光滑绝缘水平轨道相切,整个系统处在竖直向上的匀强电场中,一质量为m,电荷量为q带正电的小球以v0的初速度沿水平面向右运动,通过圆形轨道恰能到达圆形轨道的最高点C,从C点飞出后落在水平面上的D点,试求:
(1)小球到达C点时的速度vC及电场强度E;
(2)BD间的距离s;
(3)小球通过B点时对轨道的压力N.
答案
(1)从B到C过程中,由动能定理得:
(qE-mg)×2R=
mvC2-1 2
mv02,1 2
小球恰能通过最高点,
由牛顿第二定律得:mg-qE=m
,v 2C R
解得:vC=
v0,E=5 5
(g-m q
);v 20 R
(2)小球从C到D过程中,小球做类平抛运动,
水平方向:s=vCt,
竖直方向:2R=
at2,1 2
由牛顿第二定律得:mg-qE=ma,
解得:s=2R;
(3)小球在B点时,由牛顿第二定律得:
F+qE-mg=m
,解得:F=v 20 R
,6m v 20 5R
由牛顿第三定律得,小球对轨道的压力F′=
;6m v 20 5R
答:(1)小球到达C点时的速度为
v0,电场强度E=5 5
(g-m q
).v 20 R
(2)BD间的距离s=2R;
(3)小球通过B点时对轨道的压力为
.6m v 20 5R
