问题
问答题
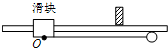
图中滑块和小球的质量均为m,滑块可在水平放置的光滑固定导轨上自由滑动,小球与滑块上的悬点O由一不可伸长的轻绳相连,轻绳长为l.开始时,轻绳处于水平拉直状态,小球和滑块均静止.现将小球由静止释放,当小球到达最低点时,滑块刚好被一表面涂有粘性物质的固定挡板粘住,在极短的时间内速度减为零,小球继续向左摆动,当轻绳与竖直方向的夹角θ=60°时小球达到最高点.求
(1)从滑块与挡板接触到速度刚好变为零的过程中,挡板阻力对滑块的冲量;
(2)小球从释放到第一次到达最低点的过程中,绳的拉力对小球做功的大小.
答案
(1)对系统,设小球在最低点时速度大小为v1,此时滑块的速度大小为v2,滑块与挡板接触前
由系统的机械能守恒定律:mgl=
mv12+1 2
mv22 ①1 2
由系统的水平方向动量守恒定律:mv1=mv2 ②
对滑块与挡板接触到速度刚好变为零的过程中,挡板阻力对滑块的冲量为:
I=mv2 ③
联立①②③解得I=m
方向向左④gl
(2)小球释放到第一次到达最低点的过程中,设绳的拉力对小球做功的大小为W,对小球由动能定理:
mgl+W=
mv12 ⑤1 2
联立①②⑤解得:W=-
mgl,即绳的拉力对小球做负功,大小为1 2
mgl.1 2
答:
(1)从滑块与挡板接触到速度刚好变为零的过程中,挡板阻力对滑块的冲量为I=m
,方向向左;gl
(2)小球从释放到第一次到达最低点的过程中,绳的拉力对小球做功的大小是-
mgl.1 2
