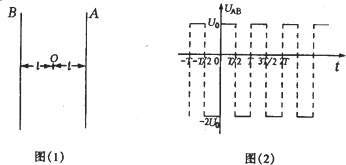
在图(l)中 A和B是真空中的两块面积很大的平行金属板,A、B间的电压 UAB随时间变化的规律如图(2)所示,在图(1)中O点到A和B的距离皆为l,在O处不断地产生电荷量为q、质量为m的带负电的微粒,在交变电压变化的每个周期T内,均匀产生300个上述微粒,不计重力,不考虑微粒之间的相互作用,这种微粒产生后,从静止出发在电场力的作用下运动,设微粒一旦碰到金属板,它就附在板上不再运动.且其电量同时消失,不影响A、B板的电势.已知上述的T=1.2×10-2s.U0=1.2×103 V,微粒电荷量q=10-7C,质量m=5×10-10kg,l=0.6m.
试求:
(l)在t=0时刻出发的微粒,会在什么时刻到达哪个极板?
(2)在t=0到t=T/2这段时间内哪个时刻产生的微粒刚好不能到达A板?
(3)在t=0到t=T/2这段时间内产生的微粒中有多少个微粒可到达A板?
(1)设在t=0时刻产生的微粒在t1时刻到达A板,且t1<.
在此过程中微粒加速度a1==| 10-7×1.2×103 |
| 5×10-10×2×0.6 |
m/s2=2×105m/s2.①

由l=a1t12得,t1==2.45×10-3s ②
t1<,所以假设成立,该微粒在t1=2.45×10-3s的时刻到达A板.
(2)设在t=0到t=这段时间内的t2时刻产生的微粒刚好不能到达A板,设此微粒在-T时间内的t3时刻到达A板时的速度刚好为零.
-t3时间内的加速度a2==| 2×10-7×1.2×103 |
| 5×10-10×2×0.6 |
=4×105m/s2.③
微粒在时刻的速度v1=a1(-t2)=a2(t3-). ④
微粒在t2-t3时间内的位移l=a1(-t2)2+a2(t3-)2 ⑤
由④⑤式得t2=4×10-3s. ⑥
t3=7×10-3s<T,所以假设成立,t2=4×10-3s时刻产生的微粒刚好不能到达A板.
(3)t2时刻产生的微粒在t3时刻到达A板时的速度为零,并立即返回,设t3-T时间内一直向B板运动,则其位移s1为:
s1=a2(T-t3)2=×4×105×(1.2×10-2-7×10-3)2=5.0m>2l ⑦
即该微粒一定会被B板吸收,在t=0时刻到t=这段时间内的t2时刻及其以后产生的微粒都不能到达A板.
所以在t=0到t=这段时间内能到达A板微粒的个数为:
n=N=×300=100.
答:(1)该微粒在t1=2.45×10-3s的时刻到达A板.
(2)在t=0到t=这段时间内t2=4×10-3s时刻产生的微粒刚好不能到达A板.
(3)在t=0到t=这段时间内能到达A板微粒的个数为100个.