已知如图,匀强电场方向水平向右,场强E=1.5×106V/m,丝线长l=40cm,上端系于O点,下端系质量为m=1.0×10-4kg,带电量为q=+4.9×10-10C的小球,将小球从最低点A由静止释放,求:
(1)小球摆到最高点时丝线与竖直方向的夹角多大?
(2)摆动过程中小球的最大速度是多大?(g=9.8m/s2)
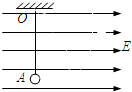
(1)在小球运动过程中,重力与电场力是恒定的,则可将此两个力等效成一个力,因此相当于小球受到拉力与等效一个力,类似于“歪摆”,这个“歪摆”.
由于已知电场力Fe=qE=4.9×10-10×1.5×106N=7.35×10-4 N
而重力G=mg=1.0×10-4×9.8N=9.8×10-4 N
因此F:G=3:4,所以摆动到平衡位置时丝线与竖直方向成37°角,因此最大摆角为74°.
(2)小球通过“最低点”即平衡位置时速度最大.在摆过程中拉力不做功,等效的力做正功,
所以由动能定理:
mgl(1-cos37°)=12+(
)23 4
mvB2-0,1 2
解之得:vB=1.4m/s.
答:(1)小球摆到最高点时丝线与竖直方向的夹角74°
(2)摆动过程中小球的最大速度是1.4m/s.
