问题
问答题
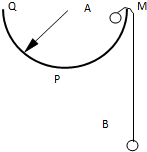
如图所示,有一半径为R的半圆形圆柱面MPQ,质量为2m的A球与质量为m的B球,用轻质绳连接后挂在圆柱面边缘.现将A球从边缘M点由静止释放,若不计一切摩擦,
求(1)A球沿圆柱面滑到最低点P时的速度大小.
(2)A球沿圆柱面滑到最低点P的过程中绳子对A,对B,对AB所组成的系统各做多少功.
答案
当A球运动到P点时,作出图象如图所示:
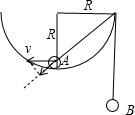
设A球的速度为v,根据几何关系可知B球的速度为
v,B球上升的高度为2 2
R2
对AB小球整体运用动能定理得:
•2mv2+1 2
m(1 2
v)2=2mgR-mg2 2
R2
解得:v=
gR
(2-4 5
)2
对A运用动能定理的:
2mgR+WA=
•2mv21 2
解得:WA=-
mgR-2 5 4 5
mgR2
对AB组成的系统,绳子的力为内力,故绳子对系统做的功为0,
所以WB=-WA=
mgR+2 5 4 5
mgR2
答:(1)A球沿圆柱面滑到最低点P时的速度大小为
gR.
(2-4 5
)2
(2)A球沿圆柱面滑到最低点P的过程中绳子对A做功为-
mgR-2 5 4 5
mgR,对B做功为2
mgR+2 5 4 5
mgR,对AB所组成的系统做功为0.2
