问题
填空题
如图所示,在水平向左的匀强电场中,一根不可伸长的绝缘细线长度为L,一端拴一个质量为m电荷量为q的带负电小球,另一端固定在O点.把小球拉到使细线水平伸直的位置A然后将小球由静止释放,小球沿弧线运动到细线与水平方向成θ=60°的位置B时速度为零.则电场强度E=______,小球运动过程中的最大速率为______.
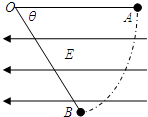
答案
由动能定理可知:
mgLsin60°-EqL(1-cos60°)=0
解得:E=
;
mg3 q
设小球在运动中细线与水平方向的夹角为α,则对任一时刻应有:
mgLsinα-EqL(1-cosα)=
mv2; 1 2
解得:v=
=2gLsinα-2 3gL(1-cosα)
=2gL(sinα+
cosα)-23
gL3 4gLsin(60°+α)-2 3gL
当α=30°时,v最大,最大值vm=
; 2gL(2-
)3
故答案为:
;
mg3 q
.2gL(2-
)3
