问题
问答题
据1951年，物理学家发现了"电子偶数"，所谓"电子偶数"就是由一个负电子和一个正电子绕它们连线的中点旋转形成的相对稳定的系统．已知正、负电子的质量均为m，普朗克常量为h，静电常量为k.
(1)若正、负电子是由一个光子和核场作用产生的，且相互作用过程中核场不提供能量，则此光子的报率必须大于某个临界值，此临界值为多大？
(2)假设"电子偶数"中，正负电子绕它们连线的中点做匀速圆周运动的轨道半径r、运动速度v及电子质量满足波尔的轨道量子化理论：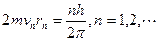
．"电子偶数"的能量为正、负电子运动的动能和系统的电势能之和，已知两正、负电子相距L时系统的电势能为
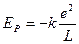．试求n=1时"电子偶数"的能量.
(3)"电子偶数"由第一激发态跃迁到基态发出的光子的波长为多大？
答案
（1）
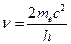（2）
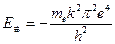(3)
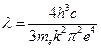
(1)由题意知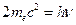
，所以。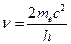
(2)"电子偶数"绕质量中心（即几何中心）转动，则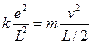
，
故"电子偶数"的总动能为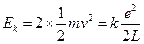
。
又已知其电势能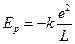
，故"电子偶数"的总能量为
。
根据波尔的轨道量子化理论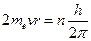
，可得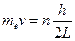
。
解之得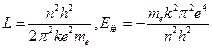
，
在n=1时有。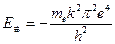
(3)"电子偶数"从第一激发态（n=2)跃迁至基态时，放出能量，可得
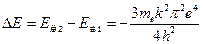，又
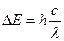，得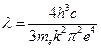。