如图所示,一薄木板斜搁在高度一定的平台和水平地板上,其顶端与平台相平,末端置于地板的P处,并与地板平滑连接.将一可看成质点的滑块自木板顶端无初速释放,沿木板下滑,接着在地板上滑动,最终停在Q处.滑块和木板及地板之间的动摩擦因数相同.现将木板截短一半,仍按上述方式搁在该平台和水平地板上,再次将滑块自木板顶端无初速释放,(设物体在板和地面接触处平滑过渡),则滑块最终将停在( )
A.P处
B.P、Q之间
C.Q处
D.Q的右侧
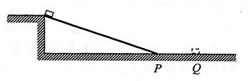
假设斜面与水平面的夹角为α,斜面的高度为h,斜面在水平方向的投影为x1
在斜面上克服摩擦力做的功 W1=μmgcosα×
=μmghcotα=μmgx1 ①h sinα
设在水平面上滑行的距离为x2
怎在水平面上克服摩擦力做的功 W2=μmgx2
整个过程克服摩擦力做得功为 W=μmgx1+μmgx2=μmg(x1+x2) ②
由此公式可知,摩擦力做得功与斜面的夹角无关,
又由于从相同的高度滑下,根据动能定理得:mgh-W=0 ③
②③联立可知,
最终还是停在Q处,故ABD错,C正确;
故选C.
