如甲图所示,长为4m的水平轨道AB与倾角为37°的足够长斜面BC在B处连接,有一质量为2kg的滑块,从A处由静止开始受水平向右的力F作用,F按乙图所示规律变化,滑块与AB和BC间的动摩擦因数均为0.25,重力加速度g取l0m/s2.求:
(1)滑块第一次到达B处时的速度大小;
(2)不计滑块在B处的速率变化,滑块到达B点时撤去力F,滑块冲上斜面,滑块最终静止的位置与B点的距离.(sin37°=0.6)
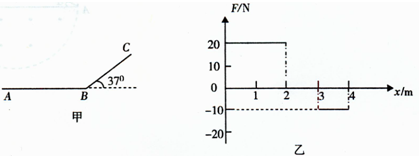
(1)由图得:0~2m:F1=20N△X1=2m;
2~3m:F2=0,△X2=1m;
3~4m:F3=10N,△X3=1m
A至B由动能定理:F1•△X1-F3•△X3-μmg(△X1+△X2+△X3)=
mvB21 2
解得vB=
m/s 10
(2)因为mgsin37°>μmgcos37°
设滑块由B点上滑的最大距离为L,
由动能定理-μmgLcos37°-mgLin37°=0-
mvB21 2
解得:L=
m 5 8
从最高点滑回水平面,设停止在与B点相距S处,
mgLin37°-μmgLcos37°-μmgs=0-0
解得:S=1m.
答:(1)滑块第一次到达B处时的速度大小为
m/s;10
(2)滑块冲上斜面,滑块最终静止的位置与B点的距离为1 m.
