有一带负电的小球，其带电荷量q=-2×10-4 C．如图所示，开始时

问题问答题

有一带负电的小球，其带电荷量q=-2×10^-4C．如图所示，开始时静止在场强E=2×10³V/m的匀强电场中的P点，靠近电场极板B有一挡板S，小球与挡板S的距离h=4cm，与A板距离H=36cm，小球的重力忽略不计．在电场力作用下小球向左运动，与挡板S相碰后电荷量减少到碰前的k倍，已知k=7/8，碰撞过程中小球的机械能没有损失．

（1）设匀强电场中挡板S所在位置的电势为零，则小球在P点时的电势能为多少？

（2）小球第一次被弹回到达最右端时距S板的距离为多少？

（3）小球经过多少次碰撞后，才能抵达A板？（已知lg

=0.058）

答案

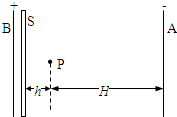
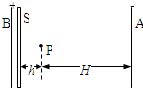
（1）SP间的电势差：U=φS-φP=Eh=2×103×0.04V=80V．

因：φ_S=0，∴φ_P=-80V，

小球在P点时的电势能：E_p=qφ_p=-2×10^-4×（-80）J=0.016J

（2）小球第一次从P到S有动能定理得：

qEh=

mv²

设小球第一次被弹回至最右端距S板的距离为h₁

有：q₁Eh₁=（kq）Eh₁=

mv²

得：h1=

h=4.6cm

（3）同理小球第二次碰撞后离S板的距离有：

h₂=

h₁=(

)2h

推得：h_n=(

)nh

当到达A板时，有：h+H=h_n

所以：n=

h+H

4+36

=17.2

所以小球经过18次碰撞后，才能抵达A板

答：（1）小球在P点时的电势能为0.016J

（2）小球第一次被弹回到达最右端时距S板的距离4.6cm

（3）小球经过18次碰撞后，才能抵达A板