B. 滑雪者从A点由静止沿斜面滑下,沿一平台滑过后水平飞离B点,最后落到地面,空间几何尺度(H、h和L)如图所示.斜面、平台与滑雪板之间的动摩擦因数为μ.假设滑雪者由斜面底端进入平台后立即沿水平方向运动,且速度大小不变.求:
(1)滑雪者从A到B的过程中,克服摩擦力做的功;
(2)滑雪者离开B点时的速度大小;
(3)滑雪者从B点开始做平抛运动,到达地面时的速度大小.
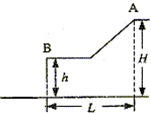
(1)设滑雪者质量为m,斜面长为s,斜面与水平面夹角为θ,滑雪者滑行过程中克服摩擦力做功:
W=μmgcosθ•s+μmg(L-scosθ)=μmgL
(2)A到B的过程,由动能定理得
mg(H-h)-μmgL=
mv21 2
故滑雪者离开B点时的速度为 v=2g(H-h-μL)
(3)滑雪者离开B点到着地过程,机械能守恒,则有:
mv2+mgh=1 2
mv′21 2
解得着地速度v′=2g(H-μL)
答:
(1)滑雪者从A到B的过程中,克服摩擦力做的功是μmgL;
(2)滑雪者离开B点时的速度大小是
;2g(H-h-μL)
(3)滑雪者从B点开始做平抛运动,到达地面时的速度大小是
.2g(H-μL)
