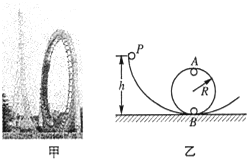
游乐场的过山车可以底朝上在圆轨道上运行,游客却不会掉下来(如图甲).我们可以把它抽象成图乙所示的由曲面轨道和圆轨道平滑连接的模型(不计摩擦和空气阻力).若质量为m的小球从曲面轨道上的P点由静止开始下滑,并且可以顺利通过半径为R的圆轨道的最高点A.已知P点与B点的高度差h=3R,求:
(1)小球通过最低点B时速度有多大?
(2)小球通过A点时对圆轨道的压力有多大?
(3)若小球在运动中需要考虑摩擦和空气阻力,当小球从P点由静止开始下滑,且刚好能通过最高点A,则小球从P点运动到A点的过程中克服摩擦和空气阻力所做的功为多少?
(1)设小球在最低点的速度为V,由动能定理得:
mgh=
mV21 2
得V=
=2gh 6gR
(2)取小球为研究对象,小球在A点的速度为VA,设轨道对小球的弹力为F,
由动能定理得:
mg(h-2R)=
mVA2 1 2
由向心力定义和牛顿第二定律得:
F+mg=mVA2 r
联立得F=mg
由牛顿第三定律得:小球对轨道的压力F′=mg
(3)设小球刚好在A点的速度为V0,由向心力定义和牛顿第二定律得:
mg=
即V0=mV02 R gR
设小球从P点运动到A点的过程中克服摩擦和空气阻力所做的功W,由动能定理得:
mg(h-2R)+W=
mV021 2
得 W=-0.5mgR
所以小球克服阻力做功0.5mgR
答:(1)小球通过最低点B时速度V=6gR
(2)小球通过A点时对圆轨道的压力F′=mg
(3)小球从P点运动到A点的过程中克服摩擦和空气阻力所做的功为0.5mgR
