问题
问答题
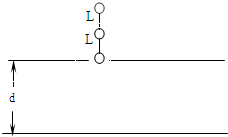
如图所示,一平行板电容器水平放置,板间距离为d,上极板开有一小孔,三个质量均为m、带电荷量均为+q的带电小球,其间用长为L的绝缘轻轩相连,处于竖直状态,已知 d=3L今使下端小球恰好位于小孔中,且由静止释放,让三球竖直下落.当下端小球到达下极板时,速度恰好为零. 试求:
(1)两极板间的电压
(2)小球运动的最大速度.
答案
(1)从开始到下端小球到达下极板,应用动能定理得:
3mgd-Eqd-Eq(d-L)-Eq(d-2L)=0 …(1)
d=3L …(2)
而E=
…(3)U d
联立解得 U=9mgL 2q
(2)当合力为零速度最大,即3mg=EQ
由(2)(3)(4)得:E=3mg 2q
联立以上两式得 Q=2q
所以第二小球进入电场时速度最大,根据动能定理得
3mgL-qEL=
•3m1 2 v 2m
解得,vm=gL
答:
(1)两极板间的电压为
.9mgL 2q
(2)小球运动的最大速度为
.gL
