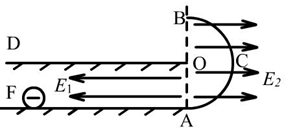
如图所示,ACB为光滑圆弧轨道其半径为R,O为其圆心,OD为水平台面.AF为光滑水平面且与圆弧ACB光滑连接.已知:在DFAO区域存在水平向左的匀强电场,场强大小为E1,AOB右侧空间存在水平向右的匀强电场,场强大小为E2,且E1=E2.在AE水平面上有一个质量为m,电荷量为q的带负电小球(可看作质点).若其重力mg=qE1 问
(1)至少从距离A点多远处无初速度释放该小球才能使其通过B点.(2)通过B点后落在水平面OD上距O点的距离在什么范围内.
(1)设至少从距离A点x1处无初速度释放该小球才能使其通过B点.
带电小球要通过B点,根据圆周运动规律,小球在圆弧轨道的等效最高点在OB右偏45°的H点上.从小球释放到H点,由动能定理得:
qE1x1-qE2
R-mg(1+2 2
)R=2 2
mv21 2
在H点,有
mg=m2 v2 R
又题意,mg=qE1=qE2.
联立以上三式得:x1=(1+
)R3 2 2
(1)小球通过B点的速度为vB.由释放到B点,由动能定理得:
qE1x1-mg2R=
m1 2 v 2B
又mg=qE1.
解得,vB=2(3
-2)gR2
小球离开B点做平抛运动,由平抛运动的规律得:
R=
gt21 2
x2=vBt
解得,x2=
R2(3
-2)2
即通过B点后落在水平面OD上距O点的距离为x2≥
R.2(3
-2)2
答:
(1)至少从距离A点(1+
)R处无初速度释放该小球才能使其通过B点.3 2 2
(2)通过B点后落在水平面OD上距O点的距离为x2≥
R.2(3
-2)2
