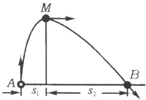
一小球自A点竖直向上抛出,在大风的情况下,若风力的大小恒定、方向水平向右,小球运动的轨迹如图所示(小球的运动可看作竖直方向的竖直上抛运动和水平方向的初速为零的匀加速度直线运动的合运动).在小球运动的轨迹上A、B两点处在同一水平线上,M点为轨迹的最高点.小球抛出的初动能为5J,小球在最高点M处的动能为2J,其它的阻力不计.求:
(1)小球水平位移S1与S2之比;
(2)小球的重力G与所受风力F的比值;
(3)小球落回到B点时的动能EKB;
(4)小球从A点到B点的运动过程中,小球动能的最小值.
(1)小球在竖直方向上做竖直上抛运动,根据对称性得知,从A点至M点和从M点至B点的时间t相等.
小球在水平方向上做初速为零的匀加速直线运动,设加速度为a,则
S1=at2
S2=a(2t)2-at2=at2
所以=
(2)由题,m=5J,得vA=
又竖直方向上,有vA=gt=t,所以=t,①
m=2J,得vM=
在水平方向上,有 vM=at=t,则得=t,②
所以①:②得=
(3)小球在水平方向上=2aS1,=2a(S1+S2)=8aS1,
故=4
小球落回到B点时的动能EKB=m=m(+)=m•4+m=13J
(4)设小球运动时间为t时动能为Ek,则
Ek=m(v0-gt)2+m(at)2
化简为 (g2+a2)t2-2v0gt+-=0
当△=0时有极值,
则4g2-4(g2+a2)(-)=0
得Ek=Ek0
由=得a=g
即Ekmin=Ek0=×5J=1.43J
答:
(1)小球水平位移S1与S2之比1:3;
(2)小球的重力G与所受风力F的比值是:;
(3)小球落回到B点时的动能EKB是13J;
(4)小球从A点到B点的运动过程中,小球动能的最小值是1.43J.