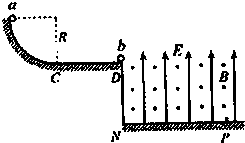
如图,半径R=0.8m的四分之一光滑圆弧轨道位于竖直平面内,与长CD=2.0m的绝缘水平面平滑连接,水平面右侧空间存在互相垂直的匀强电场和匀强磁场,电场强度E=40
,方向竖直向上,磁场的磁感应强度B=1.0T,方向垂直纸面向外.两个质量均为m=2.0×10-6kg的小球a和b,a球不带电,b球带q=1.0×10-6C的正电并静止于水平面右边缘处.将a球从圆弧轨道项端由静止释放,运动到D点与b球发生正碰,碰撞时间极短,碰后两球粘合在一起飞入复合场中,最后落在地面上的P点,已知小球a在水平面上运动时所受的摩擦阻力f=0.1mg,PN=N C
ND,取g=10m/s2.a、b均可作为质点.求3
(1)小球a与b相碰后瞬间速度的大小v;
(2)水平面离地面的高度h;
(3)从小球a开始释放到落地前瞬间的整个运动过程中,ab系统损失的机械能△E.

(1)设a球到D点时的速度为vD,从释放至D点,根据动能定理:
mgR-0.1mg×CD=
m1 2 v 2D
对a、b球,根据动量守恒定律 mvD=2mv
解得:v=
m/s=1.73m/s 3
故小球a与b相碰后瞬间速度的大小为v=1.73m/s.
(2)两球进入复合场后,由计算可知Eq=2mg
两球在洛仑兹力作用下做匀速圆周运动轨迹示意图如右图所示,洛仑兹力提供向心力:
evB=2mv2 r
由图可知:r=2h
解得:h=2
m=3.46m3
故水平面离地面的高度h=3.46m
(3)根据功能关系可知ab系统损失的机械能:
△E=0.1mg×CD+
m1 2
-v 2D
×2mv2+Eqh1 2
解得:△E=1.48×10-4J
故从小球a开始释放到落地前瞬间的整个运动过程中,ab系统损失的机械能△E=1.48×10-4J.
