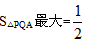问题
解答题
如图1,在△ABC中,AC=AB=2,∠A=90°,将一块与△ABC全等的三角板的直角顶点放在点C上,一直角边与BC重叠。



(1) 操作1:固定△ABC,将三角板沿C→B方向平移,使其直角顶点落在BC的中点M,如图2示。探究:三角板沿C→B方向平移的距离为 ( )。
(2)操作2:在(1)情形下,将三角板绕BC的中点M顺时针方向旋转角度α (0°<α<90°)如图3示。探究:设三角板两直角边分别与AB、AC交于P、Q,观察四边形MPAQ形状的变化,发现其面积始终不变,那么四边形MPAQ的面积S四边形MPAQ= ( )。
(3)在(2)的情形下,连PQ,设BP=x,记△APQ的面积为y,试求y关于x的函数关系式;并求x为何值时,△PQA面积有最大值,最大值是多少?
答案
解 (1)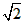
(2) S四边形MPAQ=1
(3) 连AM易证△AQM≌△BMP 则AQ=PB=x,AP=2-x
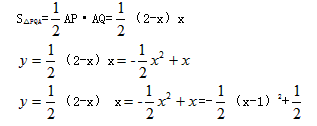
当x=1时,