某滑沙场有两个坡度不同的滑道AB和AB'(均可看作斜面),甲、乙两名旅游者分别乘两个完全相同的滑沙撬从A点由静止开始分别沿AB和AB'滑下,最后都停在水平沙面BC上,如图所示.设滑沙撬和沙面间的动摩擦因数处处相同,斜面与水平面连接处均可认为是圆滑的,滑沙者保持一定姿势坐在滑沙撬上不动.则下列说法中正确的是( )
A.甲滑行的总路程一定大于乙滑行的总路程
B.甲在B点的动能一定大于乙在B'点的动能
C.甲在B点的速率一定等于乙在B'点的速率
D.甲全部滑行的水平位移一定大于乙全部滑行的水平位移
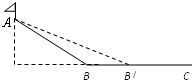
A:设甲在水平面上的位移为S,斜面长度为L,斜面所对应的水平位移为X,对甲从斜面下滑至停止这段由动能定理得:
mgh-μmgcosθL-μmgS=0
即:
mgh-μmgX-μmgS=0
整理得:
X+S=h μ
而X+S即为物体甲运动的水平位移,可见它是一个与倾角无关的量,即对甲乙来说,其水平位移是相等的,也即甲和乙是停在水平面同一点上.
由数学三角关系可以知甲的总路程大于乙的总路程.故A正确.
B:设甲下滑到斜面末端的速度为v,对甲从斜面下滑至末端由动能定理得:
mgh-μmg
=h sinθ
mv21 2
可知物体到斜面末端的动能与夹角及质量有关,由于不知道甲乙质量关系,所以无法判断谁大,故B错误.
C:从B的动能定理表达式可以整理得到:v2=2gh-
,可知速度只与夹角有关,故甲在斜面末端的速度大于乙在斜面末端的速度.2μgh sinθ
D:由A的计算知道甲乙水平位移相等.故D错误.
故选A
