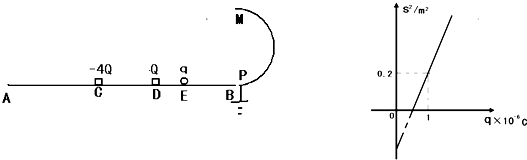
光滑绝缘水平面AB上有C、D、E三点.CD长L1=10cm,DE长L2=2cm,EB长L3=9cm.另有一半径R=0.1m的光滑半圆形金属导轨PM与水平面相连,P点接地,不计BP连接处能量损失.现将两个带电量为-4Q和Q的物体(可视作点电荷)固定在C、D两点,如图所示.将另一带电量为+q,质量m=1×104kg的金属小球(也可视作点电荷)从E点静止释放,则(感应电荷的影响忽略不计)
(1)小球在水平面AB运动过程中最大加速度和最大速度对应的位置
(2)若小球过圆弧的最高点后恰能击中放在C处的物体,则小球在最高点时的速度为多少?对轨道的压力为多大?
(3)若不改变小球的质量而改变小球的电量q,发现小球落地点到B点的水平距离s与小球的电量q,符合下图的关系,则图中与竖直轴的相交的纵截距应为多大?
(4)你还能通过图象求出什么物理量,其大小为多少?
(1)设在AB上距D点x cm处场强为0,有
=4kQ (10+x)2 kQ x2
x=10cm,即距E点8cm处
带电小球最大加速度应在场强最大处即E点处
带电小球最大速度就是场强为零点即距E点8cm处.
(2)小球从最高点水平抛出能击中C点,设速度为v,有:
v=L
=1.05m/sg 2h
设最高点压力为N,有:N+mg=m
,V2 R
N=1.025×10-4N
(3)带电小球从E开始运动,设E、B电势差为UEB,经金属轨道到从最高点下落,由
动能定理得:qUEB-2mgR=
mv2=1 2 mS2g 8R
∴当q=0时,S2=-16R2,即坐标为(0,-16R2)
即(0,-0.16m2)
所以图中与竖直轴的相交的纵截距应为-0.16m2;
(4)通过图线的斜率可求出UEB
k=
=0.36×1068RUEB mg
UEB=450V
答:(1)小球在水平面AB运动过程中,带电小球最大加速度在E点处,最大速度距E点8cm处;
(2)若小球过圆弧的最高点后恰能击中放在C处的物体,则小球在最高点时的速度为1.05m/s,对轨道的压力为1.025×10-4N;
(3)图中与竖直轴的相交的纵截距应为-0.16m2;
(4)通过图线的斜率可求出UEB,其大小为450V.
