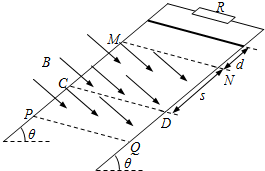
如图所示,相距为L的两条足够长的光滑平行金属导轨与水平面的夹角为θ,上端连接定值电阻R,导轨上水平虚线MNPQ区域内,存在着垂直于轨道平面向下的匀强磁场,磁感应强度为B.将质量为m、电阻为r的导体棒在距磁场上边界d处由静止释放,导体棒进入磁场运动距离s到达CD位置,速度增加到v1,此时对导体棒施加一平行于导轨的拉力,使导体棒以速度v1匀速运动时间t后离开磁场.导体棒始终与导轨垂直且电接触良好,不计导轨的电阻,重力加速度为g.求:
(1)导体棒刚进入磁场时产生的感应电动势E;
(2)导体棒到达CD位置时,电阻R上的电功率P;
(3)整个过程中回路产生的焦耳热Q.
(1)设导体棒刚进入磁场时的速度为v,由动能定理有mgdsinθ=
mv21 2
导体棒切割磁感线产生的感应电动势 E=BLv
解得 E=BL2gdsinθ
(2)导体棒到达CD位置时的感应电动势E′=BLv1
此时R上的电功率P=(
)2RE′ R+r
解得 P=B2L2
Rv 21 (R+r)2
(3)导体棒从MN运动到CD,由能量守恒定律有mgssinθ=
m1 2
-v 21
mv2+Q11 2
以v1的速度匀速运动时间t,产生的热量 Q2=
t(BLv1)2 R+r
整个过程中回路产生的热量 Q=Q1+Q2
解得 Q=mg(d+s)sinθ-
m1 2
+v 21
tB2L2 v 21 R+r
答:(1)导体棒刚进入磁场时产生的感应电动势E=BL
;2gdsinθ
(2)导体棒到达CD位置时,电阻R上的电功率P=
;B2L2
Rv 21 (R+r)2
(3)整个过程中回路产生的焦耳热Q=mg(d+s)sinθ-
m1 2
+v 21
t.B2L2 v 21 R+r
