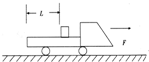
如图所示，一质量M=5kg的平板小车静止在水平地面上，小车与地面

问题问答题

如图所示，一质量M=5kg的平板小车静止在水平地面上，小车与地面间的动摩擦因数μ₁=0.1，现在给小车施加一个水平向右的拉力F=15N，经t=3s后将一质量为m=2kg的货箱，（可视为质点）无初速度地放置于平板车上，货箱与小车间的动摩擦因数μ₂=0.4，货箱最后刚好未从小车上落下，求货箱刚放上小车时离车后端的距离．

答案

对车进行受力分析：车受重力、支持力、摩擦力、拉力．

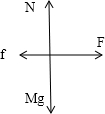
f=μ₁Mg=5N

运用牛顿第二定律：

车加速度a=

F合

15-5

m/s²=2m/s^{2
3s后的车的末速度v=at=2×3m/s=6m/s
因为刚将货箱放上去初速度为0而车的速度是6m/s所以货箱相对车而言向后运动，一直到加速到跟车的速度为止才相对静止
而此时车受到的摩擦力增加，加速度改变!
对货箱分析：货箱受到向前的摩擦力分f₁=μ₂mg=8N
对车分析：车受到地面和货箱施加的向后的摩擦力f₂=μ₁（Mg+mg）+f₁=15N．
运用牛顿第二定律得：
此时车加速度是0
货箱的加速度是4m/s²
设当ts后货箱和车的速度相同（货箱速度不会超过车）
对货箱根据v=at得：
4t=6，t=1.5s
因为货箱最后刚好未从小车上落下，所以货箱距离车后端的距离等于车移动的位移减去货箱移动的位移
在1.5s内车移动的位移为x_M=vt=9m
在1.5s内货箱移动的位移x_m=
1
2
at²=4.5m
货箱距离车后端的距离△x=x_M-x_m=4.5m
答：货箱距离车后端的距离为4.5m．}