问题
解答题
求与点M（4，3）的距离为5，且在两坐标轴上的截距相等的直线方程。
答案
解：①当截距不为零时，
设所求直线方程为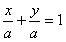
，即x+y-a=0，
因为点M（4，3）与所求直线的距离为5，
所以
，解得a=7±5
，
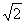所以，此时所求直线的方程为x+y-7-5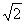
=0或x+y-7+5
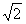=0。
②当截距为零时，
设所求直线为y=kx，
因为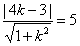
，即（4k-3）2=25（k2+1），解得k=
，
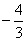所以，此时所求直线方程为y=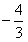
x；
综上所述，所求直线的方程为x+y-7-5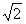
=0或x+y-7+5
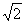=0或y=
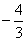x。