问题
填空题
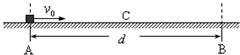
如图所示,质量为m带电量为+q的小滑块以大小为v0的初速度从A点进入宽度为d的AB绝缘水平面.当滑块运动至中点C时,速度大小为vC=
v0,从此刻起在AB区域内加上一个水平向左的强度不变的有界匀强电场(区域外不存在电场).若小滑块受到的电场力与滑动摩擦力大小相等,则滑块离开AB区域时的速度______,要使小滑块在AB区域内运动的时间达到最长,电场强度应为______.(设最大静摩擦力大小等于滑动摩擦力)3 2
答案
设滑块所受滑动摩擦力大小为f,则滑块从A点运动至C点过程,由动能定理得
f
=d 2
m(v02-vc2)----①1 2
假设最后滑块从B点离开AB区域,则滑块从C点运动至B点过程,由动能定理得
(qE1+f)
=d 2
m(vc2-vB2)------②1 2
将vc=
v0和和qE1=f代入解得3 2
vB=
v0--------③1 2
(2)要使小滑块在AB区域内运动的时间到达最长,必须使滑块运动至B点停下,然后再向左加速运动,最后从A点离开AB区域.
滑块从C点运动至B点过程,由动能定理得
(qE2+f)
=d 2
mvc2------④1 2
由①④两式可得电场强度
E2=
-----------⑤m v 20 2qd
故答案为:
v0,1 2 m v 20 2qd
