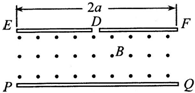
如图所示,在一对以板长为2a、板间距离为
a的平行板围成的矩形EFQP区域内有垂直于纸面向外的匀强磁场.现有一质量为m、电量为q的带正电粒子从静止开始经过电势差为U的电场加速后,从EF边的中点小孔D处垂直于EF边进入磁场,不计重力和空气阻力的影响.2 3
(1)若粒子的轨道半径为a,求磁场的磁感应强度B的大小;
(2)若改变磁感应强度的大小,使粒子恰好未碰PQ板,求粒子在磁场中运动的时间;
(3)若再次改变磁感应强度的大小,使粒子与ED板多次碰撞后刚好击中板端E点,试讨论此种情况粒子在磁场中运动的时间与碰撞次数的关系.(不计粒子与ED板碰撞的作用时间.设粒子与ED板碰撞前后,电量保持不变并以相同的速率反弹.)
(1)设粒子经电场加速射入磁场时的速度为v,
由动能定理有:qU=
m v2 ①1 2
又设当粒子的轨道半径为r1=a时,磁场的磁感应强度为B,由洛仑兹力提供向心力有:qvB=m
②v2 r1
联立①②式并代入已知量解得:B=1 a 2mU q
(2)若粒子恰好未碰PQ板,则由题意和作图知其轨道半径为:
r2=
a ③2 3
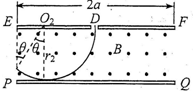
设粒子在磁场中运动轨迹所对的圆心角为α,
由图中几何关系有:
α=
+θ ④π 2
sinθ=
⑤a-r2 r2
而周期为:T=
⑥2πr2 v
粒子在磁场中运动时间为:t=
• T ⑦α 2π
联立①③④⑤⑥⑦式并解得:t=4πa 9 m 2qU
(3)设粒子运动圆周半径为r,经过n次碰撞,即经过n个半圆运动,最后一次打到E点.
有:n=
⑧a 2r
圆周运动周期:T=
⑨2πr v
粒子在磁场中运动时间:tm=n
⑩T 2
联立①⑧⑨⑩式并解得:tm=πa 2 m 2qU
显然,此种情况粒子在磁场中运动的时间与碰撞次数无关.
答:(1)若粒子的轨道半径为a,磁场的磁感应强度B的大小为1 a
;(2)若改变磁感应强度的大小,使粒子恰好未碰PQ板,求粒子在磁场中运动的时间为2mU q 4πa 9
;(3)若再次改变磁感应强度的大小,使粒子与ED板多次碰撞后刚好击中板端E点,粒子在磁场中运动的时间为m 2qU πa 2
与碰撞次数的无关.m 2qU
