如图所示，半径为R的光滑半圆环轨道与高为8R的倾角为53°的粗糙

问题问答题

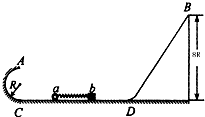
如图所示，半径为R的光滑半圆环轨道与高为8R的倾角为53°的粗糙斜面固定在同一竖直平面内，两轨道之间由一条光滑水平轨道CD相连，水平轨道与斜面间有一段圆弧过渡．在水平轨道上，轻质弹簧被小球a和滑块b挤压，处于静止状态．同时释放两物体，a球恰好能通过圆环轨道最高点A，b物块恰好能到达斜面的最高点B．已知a球质量为m，b滑块与斜面间的动摩擦因数为

，重力加速度为g，sin53°=0.8，cos53°=0.6．求：

（1）a球释放时的速度大小；

（2）b球释放时的速度大小；

（3）释放小球前弹簧的弹性势能．

答案

（1）a球过圆轨道最高点A时 mg=m

a球从C运动到A，由机械能守恒定律

+mg×2R

由以上两式求出 va=vC=

5gR

（2）b球从D运动到B，由动能定理得：

-mg•8R-μmgcos53°

sin53°

=0-

求出vb=2

5gR

（3）以a球、b球为研究对象，由动量守恒定律

mv_a=m_bv_b

求出mb=

弹簧的弹性势能 Ep=

求出 E_ρ=7.5mgR

答：

（1）a球释放时的速度大小是

5gR

；

（2）b球释放时的速度大小是2

5gR

；

（3）释放小球前弹簧的弹性势能是7.5mgR．