问题
问答题
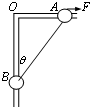
如图所示,竖直平面内有一根直角杆AOB,杆的水平部分粗糙,动摩擦因数μ=0.2,杆竖直部分光滑,两部分各套有质量均为2kg的滑环A和B,两环间用细绳相连,绳长L=1m,开始时绳与竖直杆的夹角θ为37°.现用大小为50N的水平恒力F将滑环A从静止开始向右拉动,当θ角增大到53°时,滑环A的速度为1.2m/s,求在这一过程中拉力F做的功及滑环A克服摩擦力所做的功.
某同学的解法如下:
A环向右移动的位移s=L(sin37°-cos37°)
整体分析A、B受力在竖直方向合力为零,则
FN=(mAg+mBg)
滑动摩擦力Ff=μFN
拉力所做的功WF=Fs
A环克服摩擦力所做的功Wf=Ffs
代入数据就可解得结果.
你认为该同学上述所列各式正确吗?若正确,请完成计算.若有错,请指出错在何处,并且重新列式后解出结果.
答案
该同学所列式子有错误的地方.错在A环所受支持力的分析上,因为A、B在运动过程中均有加速度,所以A、B整体竖直方向上合力不为零.
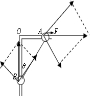
整体动能定理方程:WF-Wf-mBgh=
mAvA2+1 2
mBvB2,1 2
而vAsin53°=vB sin37°,
h=L(sin53°-sin37°),
所以WF=Fx=F(Lsin53°-Lsin37°)=10J.
Wf=2J.
答:拉力F做功为10J,克服阻力做功为2J.
