如图(甲)所示为电视机中显像管的原理示意图,电子枪中的灯丝加热阴极而逸出电子,这些电子再经加速电场加速后,从O点进入偏转磁场中,经过偏转磁场后打到荧光屏MN上,使荧光屏发出荧光形成图象,不计逸出电子的初速度和重力.已知电子的质量为m、电荷量为e,加速电场的电压为U,偏转线圈产生的磁场分布在边长为l的正方形abcd区域内,磁场方向垂直纸面,且磁感应强度随时间的变化规律如图乙所示.在每个周期内磁感应强度都是从-B0均匀变化到B0.磁场区域的左边界的中点与O点重合,ab边与OO′平行,右边界bc与荧光屏之间的距离为s.由于磁场区域较小,且电子运动的速度很大,所以在每个电子通过磁场区域的过程中,可认为磁感应强度不变,即为匀强磁场,不计电子之间的相互作用.
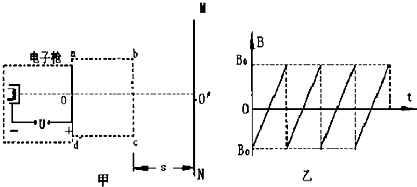
(1)求电子射出加速电场时的速度大小
(2)为使所有的电子都能从磁场的bc边射出,求偏转线圈产生磁场的磁感应强度的最大值B0
(3)荧光屏上亮线的最大长度是多少.
(1)设电子射出电场的速度为v,则根据动能定理,对电子加速过程有
mv2=eU1 2
解得v=2eU m
(2)当磁感应强度为B0或-B0时(垂直于纸面向外为正方向),
电子刚好从b点或c点射出,设此时圆周的半径为R1.
如图

所示,根据几何关系有:R2=l2+(R-
)2l 2
解得R=
L5 4
电子在磁场中运动,洛仑兹力提供向心力,因此有:evB0=m
,v2 R
解得B0=4 5l 2mU e
(3)根据几何关系可知,tanα=4 3
设电子打在荧光屏上离O′点的最大距离为d,
则d=
+s•tanα=l 2
+l 2
s4 3
由于偏转磁场的方向随时间变化,根据对称性可知,荧光屏上的亮线最大长度为D=2d=l+
s8 3
答:(1)电子射出加速电场时的速度大小为v=
.2eU m
(2)偏转线圈产生磁场的磁感应强度的最大值B0=4 5l
.2mU e
(3)荧光屏上亮线的最大长度是l+
s.8 3