问题
问答题
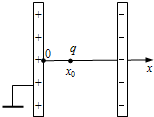
如图所示,平行板电容器两极板间有场强为E的匀强电场,且带正电的极板接地.一质量为m,电荷量为+q的带电粒子(不计重力)从x轴上坐标为x0处静止释放.
(1)求该粒子在x0处电势能Epx0.
(2)试从牛顿第二定律出发,证明该带电粒子在极板间运动过程中,其动能与电势能之和保持不变.
答案
(1)W电=qEx0…①
W电=-(Epx0-0)…②
联立①②得Epx0=-qEx0
(2)解法一
在带电粒子的运动方向上任取一点,设坐标为 x
由牛顿第二定律可得
qE=ma…④
由运动学公式得
V
=2a(x-x0)…⑤ 2x
联立④⑤进而求得:
Ekx=
mv1 2
=qE(x-x0) 2x
E=Ekx+Epx=-qEx0=Ex0
(2)解法二
在 x轴上任取两点 x1、x2,速度答:分别为 v1、v2
F=qE=ma
v
-v 22
=2a(x2-x1) 21
联立得:
mv1 2
- 22
m v1 2
=qE(x2-x1) 21
m v1 2
+(-qEx2)= 22
m v1 2
+(-qEx1) 21
Ek2+EP2=Ek1+Ep1
答:(1)该粒子在x0处电势能-qEx0
(2)该带电粒子在极板间运动过程中,其动能与电势能之和保持不变.
