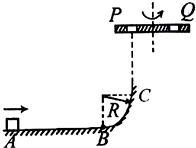
如图所示,滑块质量为m,与水平地面间的动摩擦因数为0.1,它以v0=3
的初速度由A点开始向B点滑行,AB=5R,并滑上光滑的半径为R的1/4圆弧BC,在C点正上方有一离C点高度也为R的旋转平台,沿平台直径方向开有两个离轴心距离相等的小孔P、Q,孔径大于滑块的大小,旋转时两孔均能达到C点的正上方.求:gR
(1)滑块刚到B处的速度,
(2)若滑块滑过C点后穿过P孔,求滑块过P点后还能上升的最大高度,
(3)若滑块穿过P孔后,又恰能从Q孔落下,则平台转动的角速度ω应满足什么条件?
(1)设滑块至B点时速度为vB,对滑块由A到B点应用动能定理得:
-μmg5R=
mvB2-1 2
mv021 2
解得:
vB=8gR
滑块刚到B点时的速度为
;8gR
(2)滑块从B点开始运动后机械能守恒,设滑块到达P处时速度为vp,则
mvB2=1 2
mvP2+mg2R;1 2
解得:
vP=2gR
滑块穿过P孔后再上升机械能仍守恒,设能上升的最大高度为h
由mgh=
m1 2
可得:h=2Rv 2P
滑块过P点后还能上升的最大高度为2R;
(3)滑块穿过P孔后再回到平台的时间
t=
=42vP g R g
要实现题设过程,需满足ωt=(2n+1)π
解得:ω=π(2n+1) 4
(n=0,1,2…)g R
故平台转动的角速度ω为π(2n+1) 4
(n=0,1,2…)g R