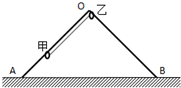
如图所示,水平面上固定光滑的等腰直角三角形支架OAB,质量m的小环甲套在OA边上,质量m的小环乙套在OB边上接近O点处,两环之间用长为L的轻绳连接.
(1)若用外力作用在小环乙上,使其沿OB边缓慢移动L,此过程外力做了多少功?
(2)两环整体的重心在绳子中点处,若将两小环从图示位置静止释放,整体重心的运动轨迹是什么形状?(本小题不需说明理由)
(3)若将两小环从图示位置静止释放,在何处两环总动能达到最大?求出此时两环速度.
(1)用外力作用在小环乙上,使其沿OB边缓慢移动L,对整体列动能定理得
WF+WG=△Ek
WF+mgsin45°L-mgsin45°(1-L)=0
WF=mgL
(2)两小环从图示位置静止释放,两环的距离不变为L,两环与0点始终构成直角三角形,斜边长度不变,两环整体的重心在绳子中点处,所以整体重心的运动轨迹是以O为圆心的圆弧
(3)根据(2)问的结果可知,在绳子水平时整体重心最低,此时整体重力势能最小,动能最大.
由动能定理得
mg-mgL=+-0
绳子水平时,两球速度相同
得v=
答:(1)此过程外力做功为mgL
(2)两环整体的重心在绳子中点处,若将两小环从图示位置静止释放,整体重心的运动轨迹是以O为圆心的圆弧
(3)在绳子水平时整体重心最低,此时整体重力势能最小,动能最大.此时两环速度为.