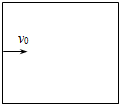
在竖直平面内有一边长为l的正方形区域处在场强为E的匀强电场中,电场方向与正方形一边平行.一质量为m、带电量为q的小球由某一边的中点,以垂直于该边的水平初速v0进入该正方形区域.当小球再次运动到该正方形区域的边缘时,具有的动能可能为( )
A.0
B.m+qEl-mgl
C.m
D.
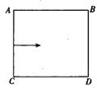
若电场方向平行于AC:
①电场力向上,且大于重力,小球向上偏转,电场力做功为qEl,重力做功为-mg,根据动能定理得:
Ek-m=qEl-mgl,得 Ek=m+qEl-mgl;
②电场力向上,且等于重力,小球不偏转,做匀速直线运动,则Ek=m.
若电场方向平行于AC,电场力向下,小球向下偏转,电场力做功为qEl,重力做功为mgl,根据动能定理得:
Ek-m=qEl+mgl,得 Ek=m+qEl+mgl;
由上分析可知,电场方向平行于AC,粒子离开电场时的动能不可能为0.
若电场方向平行于AB:
若电场力向右,水平方向和竖直方向上都加速,粒子离开电场时的动能大于0.若电场力向右,小球从D点离开电场时,有 Ek-m=qEl+mgl,则得Ek=m+qEl+mgl;
若电场力向左,水平方向减速,竖直方向上加速,粒子离开电场时的动能也大于0.故粒子离开电场时的动能都不可能为0.
故选BCD