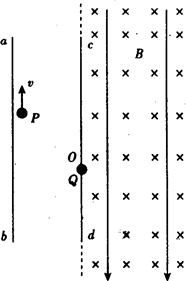
一平行板电容器的两个极板ab、cd正对竖直放置,如图所示,极板长为L.现有一电荷量大小为q、质量为m的带电质点P自紧靠ab板内侧的某点以大小为v的初速度竖直向上射出,然后以速度v从cd板的上端c处水平进入cd板右侧的正交电场、磁场中并恰好做匀速圆周运动;当带电质点P运动到cd板上小孔O处时,有另一带电质点Q由静止释放,P、Q两带电质点在小孔处发生正碰,已知Q的质量为m/3,碰撞前Q的电性与P相同且电荷量大小为q/2,碰撞后Q运动到ab板内侧的最下端b处时仍以大小为v的速度竖直离开电容器.忽略平行板电容器两端电场的边缘效应.求:
(1)电容器两板间的电场强度大小;
(2)磁场的磁感应强度大小;
(3)带电质点P最后离开平行板电容器时的速度大小.
(1)设P从出发点运动至c阶段运动的时间为t.
其中水平加速度为ax,则在水平方向上有:ax=
…①qE m
v=axt=
t…②qE m
在竖直方向上有:0-v=-gt…③
t=
…④v0 g
联立①②③得:E=
…⑤mg q
(2)设电容器两极板间的距离为d.
对P从出发点至c阶段,在水平方向上有:d=
t…⑥v+0 2
联立④⑥解得d=
…⑦v2 2g
设在正交电场、磁场中质点P做匀速圆周运动的半径为R,则qvB=mv2 R
R=
…⑧mv qB
又2R+d=l… ⑨
联立⑦⑧⑨得:B=
.4mgv q(2gl-v2)
(3)设P、Q碰撞后的速度分别为v1、v2.
由动量守恒定律得,mv=mv1+
v2m 3
设碰撞后P、Q带电量大小分别为q1、q2,则q1+q2=
q3 2
碰撞后Q在水平方向上有:d=
tv2+0 2
可得:v2=v,v1=
v2 3
0-v22=-2
dq2E m 3
得q1=
q,q2=7 6
.q 3
则碰撞后P在水平方向上的加速度ax=
=q1E m
g.7 6
它在电容器中间运动的时间仍为t,设P射出电容器时其水平速度为vx,
则vx=v1-axt=-
v1 2
则P射出电容器时的速度为vp,
vp=
=vx2+v2
v.5 2
答:(1)电容器两板间的电场强度为mg q
(2)磁场的磁感应强度大小为4mgv q(2gl-v2)
(3)带电质点P最后离开平行板电容器时的速度大小为
v.5 2
