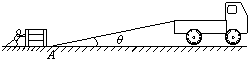
某人欲将质量m=2.0×102kg的货箱推上高h=1.0m的卡车,他使用的是一个长L=5.0m的斜面(斜面与水平面平滑连接),如图所示.假设货箱与水平面和斜面的动摩擦因数均为μ=0.10,此人沿平行于地面和斜面对货箱所施的最大推力均为Fm=4.0×102N.为计算方便可认为cosθ≈1,g取10m/s2.
(1)通过计算说明此人从斜面底端,用平行于斜面的力不能把货箱匀速推上卡车;
(2)此人要把货箱推上卡车,需要先在水平地面上推动货箱做加速运动,使货箱在斜面的底端 A处具有一定的速度,接着继续用平行于斜面最大推力Fm推货箱.为把货箱推到斜面顶端的卡车上,货箱在斜面底端的速度至少为多大?
(3)此人先以水平力,后以平行于斜面的力推货箱,推力大小总是Fm,那么,把静止于地面的货箱从水平面推到卡车上至少需做多少功?
(1)设货箱与斜面间的滑动摩擦力为f,斜面对货箱的支持力为N,斜面倾角为θ,平行于斜面用力把货箱匀速推上卡车用力为F,则:
f=μN
N=mgcosθ
F=f+mgsinθ
F=6.0×102N
因为Fm小于需要的推力6.0×102N,所以不能把货箱匀速推上卡车.
(2)欲求货箱在斜面低端的最小速度,则可设货箱到达斜面顶端时速度为零.设货箱在斜面上做匀减速运动的加速度大小为a1,货箱在斜面底端时速度至少为v,根据牛顿第二定律:
mgsinθ+μmgcosθ-Fm=ma1
解得:
a1=1.0 m/s2
根据运动学公式有:v2=2a1L
解得:v=
m/s≈3.2m/s 10
(3)要使推力做功最少,则货箱到达斜面顶端时速度为零,即货箱通过A点时速度为v,设货箱在推力Fm作用下沿水平面运动距离为s到斜面底端时,速度大小为v,根据动能定理有:
Fms-μmgs=
mv21 2
解得:s=5.0m
此人在全过程做的功为:W=Fm(s+L)=4.0×103J;
答:(1)不能将货箱推上去;
(2)货箱在斜面底端的速度至少为3.2m/s;
(3)此人在全程做的功为4.0×103J.
