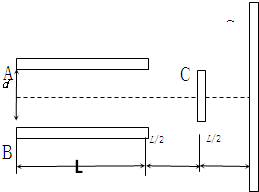
如图所示,平行正对金属板相距为d,板长为L,板间电压为U,C是宽为d的挡板,其上下两端点与A和B板水平相齐,且C离金属板与屏S的距离均为,C能吸收射到它表面的所有粒子.现让电荷量为q的带电粒子沿A、B两板中线入射,带电粒子的质量、速率均不相同,不计重力.求:
(1)带电粒子到达屏S上的宽度;
(2)初动能多大的粒子能到达屏上.
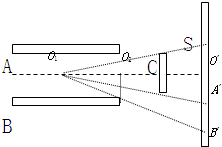
(1)带电粒子进入电场后做类平抛运动,从右侧飞出电场后做匀速直线运动,这时速度方向的反向延长线与粒子射入方向恰相交于两极板的正中央O1点,如图所示.
带电粒子到达屏S上的宽度为A´B´,由图可知:
A´B´=O´B´-O´A´
由几何关系:= 得O´B´=d
= 得O´A´=d
故带电粒子到达屏S上的宽度为d.
所以A´B´=d-d=,即带电粒子到达屏S上的宽度为.
(2)设从偏转电场边缘射出的粒子偏向角为θ1,由几何关系有:
tgθ1===,cosθ1=,
则该粒子射出电场的速度υt1==,
由动能定理得:=mυt2-mυ02=mυ0 2 (-1)
所以此粒子的动能为mυ0 2=.
设从挡板边缘射出的粒子偏向角为θ2,由几何关系有:
tgθ2===d,cosθ2=,
则该粒子射出电场的速度υt2==,
由动能定理得:=mυt22-mυ02=mυ0 2 (-1)
所以此粒子的动能为 mυ0 2=.
所以,初动能满足<EK<的粒子能到达屏上.