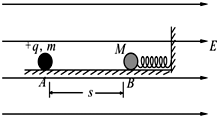
如图所示,劲度系数为k的轻弹簧,右端连在竖直墙面上,左端连着不带电的绝缘小球B,开始时B球静止在光滑绝缘水平面上.整个装置处在场强大小为E、方向水平向右的匀强电场中.现把一质量为m、带电荷量为+q的小球A,从距B球s处自由释放,A将与B发生正碰.碰撞中无机械能损失,且A球的电荷量始终不变.已知B球的质量M=2m,B球被碰后作简谐运动,其运动周期T=2π
(A、B小球均可视为质点).求:M k
(1)A球与B球第一次相碰前A的速度大小;
(2)两球第一次碰后瞬间,A球的速度v1和B球的速度v2;
(3)要使A球与B球第二次仍在B球的初始位置相碰,弹簧劲度系数k的可能取值.
(1)设A球与B球第一次碰撞前瞬间的速度为v0,由动能定理得:
qE•s=
mv21 2
解得:v0=2qEs m
(2)由于碰撞过程极短,系统的动量守恒:
mv0=mv1+Mv2
碰撞过程中无机械能损失,则有:
m1 2
=v 20
m1 2
+v 21
M1 2 v 22
联立解得:v1=-1 3
,负号表示方向向左,v2=2qEs m 2 3
,方向向右.2qEs m
(3)因|v1|<v2,要使m与M第二次碰撞仍发生在原位置,则只能是迎面相碰,所用的时间t满足:t=(n+
)T(n=0,1,2,3…)1 2
A球在电场中受电场力作用向左做减速运动至速度为0后又向右作加速运动:qEt=m(-v1)-mv1
由题知:T=2πM k
解得:k=
(n=0,1,2,3…)9π2qE(2n+1)2 4s
答:
(1)A球与B球第一次相碰前A的速度大小为
;2qEs m
(2)两球第一次碰后瞬间,A球的速度v1和B球的速度v2分别为v1=-1 3
,负号表示方向向左,v2=2qEs m 2 3
,方向向右.2qEs m
(3)要使A球与B球第二次仍在B球的初始位置相碰,弹簧劲度系数k的可能取值为:k=
(n=0,1,2,3…).9π2qE(2n+1)2 4s
