问题
问答题
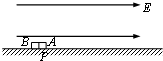
如图所示,水平桌面处有水平向右的匀强电场,场强大小E=2×104V/m,A、B是完全相同的两个小物体,质量均为m=0.1kg,电量均为q=2×10-5C,且都带负电,原来都被按在桌面上的P点.现设法使A物体获得和电场E同方向的初速vA0=12m/s,A开始运动的加速度大小为6m/s2,经τ时间后,设法使B物体获得和电场E同方向的初速vB0=6m/s(不计A、B两物体间的库仑力),求:
(1)在A未与B相遇前,A电势能增量的最大值;
(2)如果要使A尽快与B相遇,τ为多大?
答案
(1)A释放后,根据牛顿第二定律有
qE+f=ma,得f=0.2N,
A速度减到零所用时间为 t=
=2s,vAO a
经过的位移为s=
=12m,v 2AO 2a
所以在A未与B相遇前,A电势能增量的最大值为△Emax=qEs=4.8J.
(2)因为B的速度较小,要尽快相遇,对应B减速到零时与A相遇,
B的最大位移为 sB=
=3m,花时tB=v 2BO 2a
=1s,vBO a
对于A:返回时qE-f=ma′,得a′=2m/s2.
A返回走了s′=s-sB=9m,用时tA=
=3s,2s′ a
故τ=t+tA+tB=6s
答:(1)在A未与B相遇前,A电势能增量的最大值为4.8J;
(2)要使A尽快与B相遇,τ为4s.
