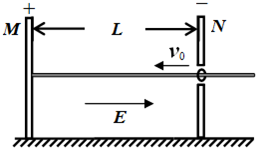
如图所示,间距为L=0.45m的带电金属板M、N竖直固定在绝缘平面上,板间形成匀强电场,场强E=1.5×104V/m.N板接地(电势为零),其中央有一小孔,一根水平绝缘细杆通过小孔,其左端固定在极板M上.现有一质量m=0.05kg,带电量q=+5.0×10-6C的带正电小环套在细杆上,小环与细杆之间的动摩擦因数为μ=0.1.小环以一定的初速度对准小孔向左运动,若小环与金属板M发生碰撞,碰撞中能量不损失(即碰后瞬间速度大小不变).设带电环大小不计且不影响金属板间电场的分布(g取10m/s2).求:
(1)带电小环以多大的初速度v0进入电场,才能恰好到达金属板M?
(2)若带电小环以初速度v1=1m/s进入电场,当其动能等于电势能时,距离N板多远?
(3)小环至少以多大的初速度v2进入电场,它在电场中运动时找不到动能与电势能相等的点?
(1)小环进入电场后,在电场力与摩擦力共同作用下减速直到M板,速度变为零,根据动能定理,有-qEL-μmgL=0-
mv021 2
得v0=
=2(qE+μmg)L m
m/s=1.5m/s2(5.0×10-6×1.5×104+0.1×0.05×10)×0.45 0.05
(2)带电小环以初速度v1=1m/s进入电场后先向左作减速运动,当其动能等于电势能时,设它距离N板为x,有
mv02-qEx-μmgx=qEx1 2
解得x=
=mv02 4qE+2μmg
m=0.125m0.05×12 4×5.0×10-6×1.5×104+2×0.1×0.05×10
还有一种情况,当小环运动到左边最远点并向右返回到小孔的过程中,也可能会出现动能等于电势能.设它向左运动的最远距离为d,根据动能定理,有-qEd-μmgd=0-
mv121 2
解得d=
=mv12 2(qE+μmg)
m=0.2m0.05×12 2×(5.0×10-6×1.5×104+0.1×0.05×10)
当其动能等于电势能时,设它距离N板为y,有qE(d-y)-μmg(d-y)=qEy
解得y=
=(qE-μmg)d 2qE-μmg
m=0.05m(5.0×10-6×1.5×104-0.1×0.05×10)×0.2 2×5.0×10-6×1.5×104-0.1×0.05×10
(3)小环以初速度v2进入电场后,若它运动到M板时的动能大于其电势能,则它在电场中运动时找不到动能与电势能相等的点,有
mv22-(qE+μmg)L>qEL1 2
得v2>
=2(2qE+μmg)L m
/s=2(2×5.0×10-6×1.5×104+0.1×0.05×10)×0.45 0.05
m/s3.6 ≈1.9m/s
答:(1)带电小环以初速度1.5m/s进入电场,才能恰好到达金属板M;
(2)若带电小环以初速度v1=1m/s进入电场,当其动能等于电势能时,距离N板的距离为0.125m或0.05m;
(3)小环至少以1.9m/s的初速度进入电场,它在电场中运动时找不到动能与电势能相等的点.
