问题
问答题
如图所示,质量为m=0.2kg的小物体放在光滑的
圆弧上端,圆弧半径R=55cm,下端接一长为1m的水平轨道AB,最后通过极小圆弧与倾角α=37°的斜面相接,已知物体与水平面和斜面轨道的动摩擦因数均为0.1,将物体无初速度释放,求:1 4
(1)物体第一次滑到水平轨道与右侧斜面轨道交接处的速度大小
(2)物体第一次滑上右侧斜轨道的最大高度(取g=10m/s2,cos37°=0.8,sin37°=0.6)
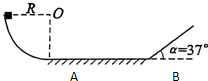
答案
已知m=0.2kg,k=0.55m,SAB=1m,m=0.1 α=37°
(1)小物体内圆弧上端到B点的过程中,由动能定理有
mgR•μmgSAB=
m1 2
θ…(1)υ 2B
=2gR-2μgSAB=9…(2)υ 2B
υB=3m/s…(3)
(2)设物体第一次滑上右侧轨道最大高度为H
此时物体离B点的距离为S,由几何关系有
=sinα…(4)H S
由动能定理有-μmgcosα•S-mgH=0-
m1 2
…(5)υ 2B
将(4)式代入(5)式 有
H=
≈0.40m27 64
答:(1)物体第一次滑到水平轨道与右侧斜面轨道交接处的速度大小是3m/s
(2)物体第一次滑上右侧斜轨道的最大高度是0.40m
