两块竖直放置的平行金属板A、B,相距d=1.0m,两板间电压为U=2500V,O点与两板距离相等.在O点有一放射源,释放质量m=2.5×10-3kg、电荷量q=1.0×10-5C的带正电微粒.过O点以半径R=0.25m作一圆,圆心O′在过O点右下方45°的直线上.P、M、S、N分布在圆周上,O′S与OO′垂直,∠OO′P=θ,∠MO′S=∠SO′N=α=30°. 不计电荷间的相互作用,取 g=10m/s2.求:
(1)初速度为零的微粒运动到平行板的动能;
(2)初速度υ0=2.0m/s,方向与x′ox成45°角斜向左上方的微粒打到平行板的时间;
(3)初速度大小不等,方向均与xox′成45°角斜向右上方,经过一段时间通过P点的微粒初速度υ0与θ的关系;并确定在穿过圆周MSN段的微粒中,穿越时的最大动能和最小动能.

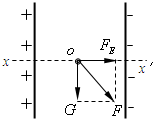
(1)带电微粒在电场中受重力和电场力FE=qE=2.5×10-2N
G=mg=2.5×10-2N
则F合=
=2.5FE2+G2
×10-2N2
因为FE=G,所以合力方向与水平方向成45°角斜右向下,
如图所示.
W合=△Ek
Ek=F×
合×2
=2.5×10-2Jd 2
(2)带电微粒射出后,沿+y轴做匀减速运动,如图所示.
xx′:F合=ma
最大位移为:s1=
=υ0 2 2a
m2 10
从O点沿+y方向离极板的距离为:s=1 2
d=2 5 10
m2
因为s1,s,所以微粒运动一段后,没有打到左极板又回头运动,最后打到右极板.
t1=
=υ0 a 1 10
s2
t2=
=2(s1+s) a 1 5
s3
t=t1+t2=(1 5
+3 1 10
)s2
(3)沿着初速度方向,微粒做匀速直线运动:则有Rsinθ=υ0t
垂直于初速度方向,微粒做初速度为零的匀加速度直线运动:则有R-Rcosθ=1 2
gt22
由以上三式得υ0=
=gRsin2θ
(1-cosθ)2
g(1+cosθ)2 8
由上式结论得粒子从O点出发时的动能为
mυ02=1 2
mg(1+cosθ)2 16
则经过P点时的动能为:EKP=
mg(R-Rcosθ)+2
mυ02=1 2
mg(5-3cosθ)2 16
可以看出,当θ从00变化到1800,微粒穿越圆周时的动能逐渐增大,因此穿过M点的微粒动能最小,穿过N点的微粒动能最大.
最小动能为:EKM=
mg(5-3cos600)≈7.7×10-3J2 16
最大动能为:EKN=
mg(5-3cos1200)≈0.0144J2 16
答:(1)初速度为零的微粒运动到平行板的动能2.5×10-2J;
(2)初速度υ0=2.0m/s,方向与x′ox成45°角斜向左上方的微粒打到平行板的时间
S;2
+3 2 10
(3)初速度大小不等,方向均与xox′成45°角斜向右上方,经过一段时间通过P点的微粒初速度υ0与θ的关系;并确定在穿过圆周MSN段的微粒中,穿越时的最大动能7.7×10-3J和最小动能1.44×102J.
