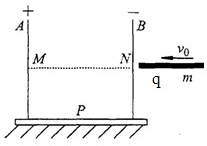
如图所示;“U”形框架由两平行金属板A、B和绝缘底座P组成,在金属板A、B上同一高度处开有两个小孔M、N,并在M、N之间固定一绝缘光滑平板,整个装置静止固定在水平面上.两平行金属板A、B接上电压为150KV的稳压电源,两金属板间距为d=0.1m.现有一电荷分布均匀的带电量为q=5×10-5C,质量为m=0.01kg,长度为l=0.04m的绝缘橡胶棒以v0=10
m/s的速度由右边小孔水平滑入“U”形框架中,设绝缘棒的电荷量对“U”形框架内的电场没有影响.问:3
(1)橡胶棒刚好全部进入“U”形框架内的加速度
(2)橡胶棒刚好全部进入“U”形框架内的速度.
(3)橡胶棒与“U”形框架相互作用过程中增加的最大电势能.
(1)金属板间的电场强度为E=
=U d
V/m=1.5×106V/m150×103 0.1
由牛顿第二定律得:a=
=qE m
m/s2=7.5×103m/s25×10-5×1.5×106 0.01
(2)设带电橡胶棒刚好全部进入“U”形框架时,则由动能定理:
-
L=qE 2
mv2-1 2
m1 2 v 20
解得:v=
=
-v 20 qEL m
m/s=0m/s(10
)2-7.5×103×0.043
(3)增加电势能的最大值等于动能减小的最大值:
△Ep=△Ek=
m1 2
=v 20
×0.01×300J=1.5J1 2
答:
(1)橡胶棒刚好全部进入“U”形框架内的加速度为7.5×103m/s2.
(2)橡胶棒刚好全部进入“U”形框架内的速度是0.
(3)橡胶棒与“U”形框架相互作用过程中增加的最大电势能是1.5J.
