问题
多选题
在竖直平面内.一根光滑金属杆弯成如图所示形状,相应的曲线方程为y=2.5cos(kx+
π)(m),式中k=1m-1.将一质量为lkg的光滑小环套在该金属杆上,在P(-2 3
,0)点给小环以平行于杆、大小为10m/s的初速,让小环沿杆向+x方向运动,取g=10m/s2.关于小环的运动,下列说法正确的是( )π 6
A.金属杆对小环不做功
B.小环沿x轴方向的分运动为匀速运动
C.小环到达金属杆的最高点时的速度为5
m/s2
D.小环到达Q=(π 3m,-2.5m)点时的速度为10
m/s2 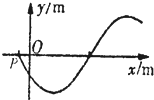
答案
A、金属杆对小环的弹力与小环的速度方向始终垂直,所以金属杆对小环不做功.故A正确.
B、对小环进行受力分析,小环受重力和金属杆对小环的弹力,将重力分解,小环实际合力方向斜向下,即小环的实际加速度方向也是斜向下.因此小环在水平方向也有了分加速度,所以小环沿x轴方向的分运动不可能是匀速运动.故B错误.
C、根据机械能守恒得:
m1 2
=mgh+v 20
mv2,h=2.5m,代入解得,v=51 2
m/s.故C正确.2
D、由机械能守恒得:
m1 2
=-mghQ+v 20
m1 2
,hQ=-2.5m,代入解得,vQ=5v 2Q
m/s.故D错误.6
故选AC
