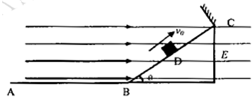
如图所示,光滑绝缘水平面AB与倾角θ=370,长L=6m的绝缘斜面BC在B处圆滑相连,在斜面的C处有一与斜面垂直的弹性绝缘挡板,质量m=0.5kg、所带电荷量q=5x10-5C的绝缘带电滑块置于斜面的中点D,整个空间存在水平向右的匀强电场,场强E=2xlO5N/C,现让滑块以v0=12m/s的速度沿斜面向上运动.设滑块与挡板碰撞前后所带电荷量不变、速度大小不变,滑块和斜面间的动摩擦因数μ=0.1,求:
(1)滑块第一次与挡板碰撞时的速度大小;
(2)滑块第一次与挡板碰撞后能达到左端的最远点离B点的距离;
(3)滑块运动的总路程.
(1)滑块从D到C的过程中,根据动能定理可得:
qEcosθ•
-mgsinθ•L 2
-Ff•L 2
=L 2
m1 2
-v 2C
m1 2 v 2D
而滑动摩擦力:Ff=μ(mgcosθ+qEsinθ)
解得vC=
m/s=8192
m/s3
(2)设滑块左侧最远点与B相距x1,滑块从C到左侧的最远处的过程中,
根据动能定理:mgsinθ•L-qE(Lcosθ+x)-Ff•L=0-
m1 2 v 2C
解得x1=1.2m
(3)当滑块在斜面BC上滑行L时,滑块与斜面的摩擦产生的热量:Q=Ff•L=6J
第二次碰撞后回到水平面时与原来相比向右移动的距离x′=
=1.2m 2Q qE
所以滑块第二次碰后刚好回到B点,
根据滑块受力的情况有:qEcosθ>mgsinθ+Ff
故滑块最终停在C处,假设滑块在斜面上运动的总路程为x2,
根据动能定理:qEcosθ•
-mgsinθ•L 2
-Ff•x2=0-L 2
m1 2 v 20
解得:x2=51m
所以滑块运动的路程:s=2x1+x2=53.4m
答:(1)滑块第一次与挡板碰撞时的速度大小为8
m/s;3
(2)滑块第一次与挡板碰撞后能达到左端的最远点离B点的距离1.2m;
(3)滑块运动的总路程53.4m.
