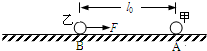
如图所示,带正电的甲球固定在足够大的光滑绝缘水平面上的A点,其带电量为Q;质量为m、带正电的乙球在水平面上的B点由静止释放,其带电量为q;A、B两点间的距离为l0.释放后的乙球除受到甲球的静电力作用外,还受到一个大小为F=
(k为静电力常数)、方向指向甲球的恒力作用,两球均可视为点电荷.kQq 4l02
(1)求乙球在释放瞬间的加速度大小;
(2)求乙球的速度最大时两个电荷间的距离;
(3)若乙球运动的最大速度为vm,试求乙球从开始运动到速度为vm的过程中电势能的变化量;
(4)请定性地描述乙球在释放后的运动情况(说明速度的大小变化及运动方向的情况).
(1)根据牛顿第二定律得,ma=
-F kQq l02
可解得a=
.3kQq 4ml02
(2)当两个力大小相等时,乙球的速度最大,
F=
=kQq 4l02
可解得x=2l0kQq x2
(3)
mvm2-0=W电-WF,1 2
W电=
mvm2+WF=1 2
mvm2+Fl0=1 2
mvm2+1 2 kQq 4l0
静电力做正功,电势能减少了
mvm2+1 2 kQq 4l0
(4)乙球先做远离甲的运动,速度先增大后减小,然后又反向做速度先增大后减小的运动,返回到释放点B后,再重复前面的运动,之后就在B点和最远端之间做往复运动.
答:(1)乙球在释放瞬间的加速度大小为
.3kQq 4ml02
(2)乙球的速度最大时两个电荷间的距离为2l0.
(3)乙球从开始运动到速度为vm的过程中电势能的变化量为
mvm2+1 2
.kQq 4l0
(4)乙球先做远离甲的运动,速度先增大后减小,然后又反向做速度先增大后减小的运动,返回到释放点B后,再重复前面的运动,之后就在B点和最远端之间做往复运动.
